Con los dos resultados anteriores demostrados, tenemos las bases para indicar los razonamientos para deducir que los cuatro problemas clásicos no se pueden resolver.
En la descripción dada del teorema 2 vemos que cualquier número construible es un número algebraico, es decir, un número que es solución de alguna ecuación algebraica con coeficientes racionales, como se vio en la sección 4.9.
En 1882, Ferdinand von Lindemann demostró que el número π es trascendental, o lo que es lo mismo, que no es solución de ninguna ecuación algebraica con coeficientes racionales. Si se quiere cuadrar el círculo, lo que se busca es encontrar la longitud del lado de un cuadrado que tiene la misma área que la de un círculo dado, por ejemplo, el círculo con radio 1, que posee un área de π, como se vio en la sección 2.9. Por lo tanto, se busca construir la longitud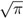 
. Si pudiéramos construir esta longitud, entonces también podríamos hacerlo con su cuadrado, es decir π, lo que es imposible por el teorema de Lindemann. Así se muestra que no es posible cuadrar el círculo.
La imposibilidad de cuadrar el círculo es la última de las cuatro demostraciones, pero la indicamos primero dado que, conceptualmente, es la más clara. Veamos ahora la duplicación del cubo.
Si tenemos un cubo dado con aristas de longitud ℓ, entonces el volumen es de ℓ3. El cubo que tiene el doble de volumen presenta aristas de longitud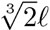 
. Para hallar esta longitud con regla y compás, debemos construir 
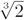dado que podemos multiplicar. Sin embargo, según el teorema 2 sólo podemos construir raíces cuadradas, no cúbicas. Pero esto no es suficiente: ¿por qué no es posible que alguna expresión que sólo involucra raíces cuadradas sea igual a 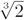? Para resolver lo anterior, necesitamos algunas herramientas de la teoría de campos.
En la sección 4.9 consideramos campos intermedios como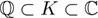 
, es decir, campos K contenidos en los números complejos 
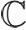y que también contienen los números racionales 
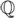. Un campo así surgió como campo de descomposición de algún polinomio f(x) y siempre tiene una dimensión sobre 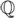. La dimensión de campos generaliza la idea del "número de coordenadas que se usan para describir una ubicación": en la recta basta una coordenada, en el plano se requieren dos y en el espacio tres. Para usar coordenadas se requiere de un origen y de ejes.
Por ejemplo, en los números complejos tenemos dos ejes: el real y el imaginario. Cualquier número complejo a + bi se expresa con dos coordenadas reales a y b. En otras palabras, cualquier número complejo es combinación con coeficientes reales de los números complejos 1 e i .
Si consideramos ahora una situación de un campo de descomposición K sobre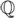, entonces fijamos k1, …, kd ∈ K y consideramos combinaciones lineales, como en:
q1k1 + q2k2 +…qnkn, (40)
con coeficientes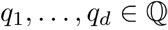 
. La dimensión de K sobre 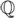es, entonces, el mínimo número d tal que existen elementos k1, …, kd ∈ K llamados base, con la propiedad de que cualquier elemento de K es combinación lineal (40) para algunos coeficientes q1, …,qd . Esta dimensión se denota por 
. Se demuestra que, cualesquiera dos bases, siempre tienen la misma cardinalidad. Además, 
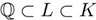si entonces:
(41)
Una consecuencia del Teorema 4.10 es que la dimensión sobre 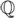de cualquier campo K que consiste en números construibles es una potencia de 2, dado que en cada paso, al aumentar una raíz cuadrada, se aumenta por un factor de 2. El campo de descomposición L de f(x)= x3 – 2, que contiene la raíz 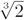, tiene dimensión 3 sobre 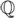, por lo tanto, una base es:
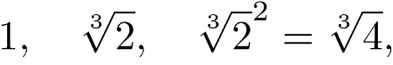(42)
y, por lo tanto, cualquier base tiene cardinalidad 3. Si suponemos que 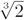es un número construible, entonces este número pertenece a un campo K que tiene dimensión 
sobre 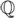para algún t. Pero si K contiene 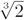, entonces también la contiene su cuadrado y, por lo tanto, la base (42). Por consiguiente, tenemos ahora las siguientes inclusiones de campos 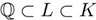, pero 
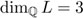y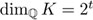 
, lo que contradice la igualdad (41).
Todo lo anterior muestra que 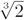no es construible y, por lo tanto, no es posible construir sólo con regla y compás el lado de un cubo que tenga el doble de volumen de un cubo dado.
Un argumento muy similar muestra que los otros dos problemas clásicos tampoco tienen solución con regla y compás: si queremos trisecar un ángulo α conocido debemos construir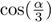 
o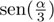 
. Para ello, requerimos de una identidad trigonométrica que se deriva de la fórmula de Euler:
(43)
donde e es el número de Euler —otro número trascendente— cuyo valor aproximado es 2.7182818284. Al elevar (43) al cubo, se obtiene:
Si comparamos las coordenadas, tenemos, después de sustituir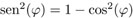 
y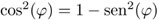 
, respectivamente, las siguientes identidades para el triple de ángulo:
(44)
(45)
Podemos usar estas fórmulas para calcular 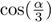, si sustituimos 
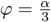en (44):
(46)
Dado que el ángulo α ya está construido, podemos hallar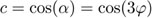 
con regla y compás, y debemos resolver la ecuación (46) en la incógnita 
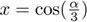, es decir, tenemos que resolver la ecuación cúbica:
En la sección 4.2 calculamos la solución y vimos que había que calcular raíces cúbicas. Si no se trata de ángulos muy particulares,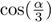no será construible. Por ejemplo, cos (20°) no es construible.
Por ello, el problema de la trisección de ángulos no se puede resolver con regla y compás. Por la misma razón, tampoco se pueden construir polígonos con cualquier número de lados pues, por ejemplo, para construir un polígono con lados, tendríamos que construir primero el cos (20°), que es imposible como acabamos de ver.
Así concluimos el recuento de una larga historia de búsqueda por la solución de algo que nunca fue posible. Los problemas clásicos no tienen solución mientras se mantenga la restricción de que las herramientas de construcción sean regla y compás, únicamente. Para comprender la imposibilidad, es necesario salir del ambiente de las construcciones: es necesario formular qué quiere decir el construir con regla y compás en un lenguaje que permite una vista distinta y que, en nuestro caso, fue el lenguaje algebraico con el uso de las herramientas de la teoría de campos. Ver que algo es imposible requiere de cierta distancia y reflexión y, en esta situación particular, una considerable cantidad de abstracción. Por ello, no debe sorprender que muchos aficionados han seguido y siguen intentando resolver alguno de los problemas y presentan construcciones ingeniosas para cuadrar el círculo, todas ellas falsas como ahora sabemos.
